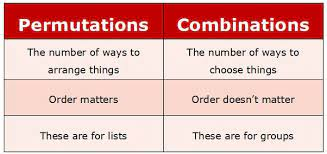
Permutation and combination are the ways to represent a group of objects by selecting them in a set and forming subsets. It defines the various ways to arrange a certain group of data. When we select the data or objects from a certain group, it is said to be permutations, whereas the order in which they are represented is called combination. Both concepts are very important in Mathematics.
Permutation and combination are explained here elaborately, along with the difference between them. We will discuss both the topics here with their formulas, real-life examples and solved questions. Students can also work on Permutation And Combination Worksheet to enhance their knowledge in this area along with getting tricks to solve more questions.
What is Permutation?
In mathematics, permutation relates to the act of arranging all the members of a set into some sequence or order. In other words, if the set is already ordered, then the rearranging of its elements is called the process of permuting. Permutations occur, in more or less prominent ways, in almost every area of mathematics. They often arise when different orderings on certain finite sets are considered.
What is a Combination?
The combination is a way of selecting items from a collection, such that (unlike permutations) the order of selection does not matter. In smaller cases, it is possible to count the number of combinations. Combination refers to the combination of n things taken k at a time without repetition. To refer to combinations in which repetition is allowed, the terms k-selection or k-combination with repetition are often used. Permutation and Combination Class 11 is one of the important topics which helps in scoring well in Board Exams.
Permutation and Combination Formulas
There are many formulas involved in permutation and combination concepts. The two key formulas are:
Permutation Formula
A permutation is the choice of r things from a set of n things without replacement and where the order matters.
nPr = (n!) / (n-r)!
Combination Formula
A combination is the choice of r things from a set of n things without replacement and where order does not matter.

Learn how to calculate the factorial of numbers here.
Difference Between Permutation and Combination
| Permutation | Combination |
|---|---|
| Arranging people, digits, numbers, alphabets, letters, and colours | Selection of menu, food, clothes, subjects, team. |
| Picking a team captain, pitcher and shortstop from a group. | Picking three team members from a group. |
| Picking two favourite colours, in order, from a colour brochure. | Picking two colours from a colour brochure. |
| Picking first, second and third place winners. | Picking three winners. |
Uses of Permutation and Combination
A permutation is used for the list of data (where the order of the data matters) and the combination is used for a group of data (where the order of data doesn’t matter).
Solved Examples of Permutation and Combinations
Example 1:
Find the number of permutations and combinations if n = 12 and r = 2.
Solution:
Given,
n = 12
r = 2
Using the formula given above:
Permutation:
nPr = (n!) / (n-r)! =(12!) / (12-2)! = 12! / 10! = (12 x 11 x 10! )/ 10! = 132
Combination:
Example 2:
In a dictionary, if all permutations of the letters of the word AGAIN are arranged in an order. What is the 49th word?
Solution:
| Start with the letter A | The arranging the other 4 letters: G, A, I, N = 4! = 24 | First 24 words |
| Start with the letter G | arrange A, A, I and N in different ways: 4!/2! = 12 | Next 12 words |
| Start with the letter I | arrange A, A, G and N in different ways: 4!/2! = 12 | Next 12 words |
This accounts up to the 48th word. The 49th word is “NAAGI”.
Example 3:
In how many ways a committee consisting of 5 men and 3 women, can be chosen from 9 men and 12 women?
Solution:
Choose 5 men out of 9 men = 9C5 ways = 126 ways
Choose 3 women out of 12 women = 12C3 ways = 220 ways
Total number of ways = (126 x 220)= 27720 ways
The committee can be chosen in 27720 ways.
Permutation and Combination – Practice Questions
Question 1: In how many ways can the letters be arranged so that all the vowels come together? Word is “IMPOSSIBLE.”
Question 2: In how many ways of 4 girls and 7 boys, can be chosen out of 10 girls and 12 boys to make the team?
Question 3: How many words can be formed by 3 vowels and 6 consonants taken from 5 vowels and 10 consonants?
From the above discussion, students would have gained certain important aspects related to this topic. To gain further understanding of the topic, it would be advisable that students should work on sample questions with solved examples. To learn more about different maths concepts, register with BYJU’S today.
Frequently Asked Questions on Permutations and Combinations
What do you mean by permutations and combinations?
A permutation is an act of arranging objects or numbers in order.
Combinations are the way of selecting objects or numbers from a group of objects or collections, in such a way that the order of the objects does not matter.
Give examples of permutations and combinations.
An example of permutations is the number of 2 letter words that can be formed by using the letters in a word say, GREAT; 5P_2 = 5!/(5-2)!
An example of combinations is in how many combinations we can write the words using the vowels of the word GREAT; 5C_2 =5!/[2! (5-2)!]
What is the formula for permutations and combinations?
The formula for permutations is: nPr = n!/(n-r)!
The formula for combinations is: nCr = n!/[r! (n-r)!]
What are the real-life examples of permutations and combinations?
Arranging people, digits, numbers, alphabets, letters, and colours are examples of permutations.
Selection of menu, food, clothes, subjects, the team are examples of combinations.
Write the relation between permutations and combinations.
nCr = nPr/r!
Give the applications of permutation and combination in mathematics.
In Mathematics, the concept called “permutation and combinations” are applied in probability, relations and functions, set theory and so on.
What is the factorial formula?
The factorial formula is used in the calculation of permutations and combinations, which is obtained by taking the product of all numbers in the sequence (i.e., from 1 to n). For example, 3! = 3 × 2 × 1 = 6.
What does nCr represent?
nCr represents the number of combinations from “n” objects taken “r” at a time.